In our last post, pendulums were the main subject. As we mentioned apart from the obvious scientific interest this “device” served for a long time as a time keeping method. More precisely from 1965 until the 1930s.
The pendulum clocks were using a swinging weight as a “timekeeping element”.
It worked because pendulums are harmonic oscillators, meaning that they swing back and forth in a precise time interval depending on their length, and they are resistant to swinging at other rates.
These clocks in order to function properly, needed to be stationary, because movement and accelerations would affect the motion of the pendulum. They had these five parts that made them work.
i) A power source (which is either a weight on a cord that turns a mainspring), ii) a gear train (that steps up the speed of the power so that the pendulum can use it), iii) an escapement (that gives the pendulum precisely timed impulses to keep it swinging and which releases the gear train wheels to move forward a fixed amount at each swing) which is the one that causes the “ticking” sound of an operating pendulum clock.
Of course it needs iv) a pendulum and v) an indicator or dial that records how often the escapement has rotated and therefore how much time has passed. Well a “clock face”.
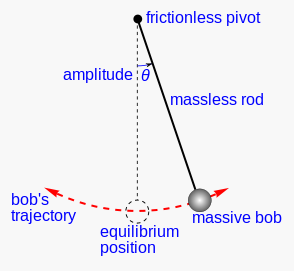
A so-called “simple pendulum” is an idealization of a “real pendulum” but in an isolated system. The period of a simple harmonic motion depends on the semi-amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical) and the length of the pendulum. Under the small-angle approximation, the period is independent of the amplitude θo.
For amplitudes beyond the small angle approximation, one can compute the exact period by first inverting the equation for the angular velocity obtained from the energy method (The integral diverges as θo approaches the vertical).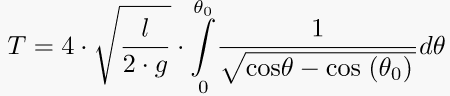
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.
