In mathematics, a series is, informally speaking, the sum of the terms of an infinite sequence. The sum of a finite sequence has defined first and last terms, whereas a series continues indefinitely. Apart from awesome, they are also super useful.
 

1. Arithmetic progression

An arithmetic progression  is a sequence of numbers such that the difference between the consecutive terms is constant and is calling common difference. The behavior of the arithmetic progression depends on the common difference . If the common difference is:
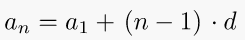
Positive, the members (terms) will grow towards positive infinity.
Negative, the members (terms) will grow towards negative infinity.

2. Fibonacci numbers

The famous Fibonacci numbers are a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms.
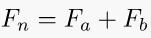
The Fibonacci numbers are the archetype of a linear, homogeneous recurrence relation with constant coefficients. Fo=0, F1=1
We obtain the sequence of Fibonacci numbers which begins: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

3. Geometric mean of two numbers

The geometric mean is defined as the square root of the product of the numbers. It only applies either to positive numbers or both negative numbers.

4. Geometric progression (nth term)

A geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. The n-th term of a geometric sequence can be calculated by the initial value and common ratio of the progression.

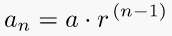
5. Geometric series (sum of the numbers)

The sum of the numbers in a geometric progression can be calculated by the initial value and common ratio of the progression.

6.  Standard deviation of any arithmetic progression

This Equation is under the 1st formulas rules. But you should know that the standard deviation of any arithmetic progression can be calculated by the nth term of the sequence. In statistics and probability theory, the standard deviation measures the amount of variation or dispersion from the average.

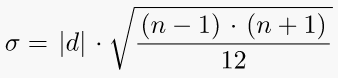
7. Sum of consecutive (pyramidal) squares

In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square base. Square pyramidal numbers also solve the problem of counting the number of squares in an n × n grid. The sum of the squares of any number of consecutive integers starting with 1. 
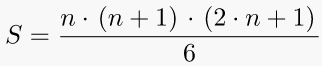
1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819 …

8. Sum of consecutive (triangular) cubes

In number theory, the sum of the first n cubes is the square of the nth triangular number. The sequence of squared triangular numbers is 0, 1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, ... (sequence A000537 in OEIS).
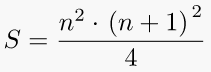
These numbers can be viewed as figurate numbers, a four-dimensional hyperpyramidal generalization of the triangular numbers and square pyramidal numbers. This is also called Nicomachus’s Theorem

9. Sum of the infinite terms

An infinite geometric series is an infinite series whose successive terms have a common ratio. Such a series converges if and only if the absolute value of the common ratio is less than one (|r| < 1). Its value can then be computed from the finite sum formula.

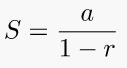
10. Triangular number

A triangular number or triangle number counts the objects that can form an equilateral triangle. The nth triangle number is the number of dots composing a triangle with n dots on a side, and is equal to the sum of the n natural numbers from 1 to n. The sequence of triangular numbers (sequence A000217 in OEIS), starting at the 0th triangular number, is: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406 …

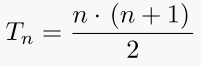
Bonus: Maclaurin series 

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function’s derivatives at a single point. If the Taylor series is centered at zero, then that series is also called a Maclaurin series. In this LINK you can find all the Maclaurin Series in our database.

You can try to search whatever you want just by clicking on the “Browse Formulas” button on the top left of your screen.

If you need any help, you will find some in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.