Earlier this week we talked about Half-Life. The bestselling-award winning Video Game, as long as the formula that describes Half-Life in Chemistry.

Valve’s video game is a Legend not only due to its initial success and the dozens of awards it won. It’s because of what happened after.

Half-Life’s post release impact is unquantifiable. Countless games have been influenced directly – or not. The revolutionary way of making the experience unbroken from start to finish, without breaking down the story in chapters or platforms.
Also, the scenery it created was a leap for the genre which was traditionally taking place into a maze. Crawling into air vents, or wondering inside huge industrial spaces made the game much more believable than its predecessors, and lead the way for all the other First Person Shooters you have played. Famous games like Doom 3, F.E.A.R., and Bioshock have roots in the techniques first seen in Half-Life.

While today its graphics are outdated, and its innovations are taken for granted its bloodline is dominating the online First Person Shooter genre.
A year after the release of Half-Life, Valve introduced the world to the most popular Online FPS game ever. Counter Strike.
Two teams (Terrorists and Counter Terrorists) are facing each other in a platform. Terrorists have a bomb or hostages and the others must defuse it or save them unharmed.
The game is so popular that it even has a World Championship with Shout Casters, audience and everything.

In Quantum Mechanics Half-Life is described by the Exponential decay equation which is the one on the left. A quantity is said to be subject to exponential decay if it decreases at a rate proportional to its value. If the decaying quantity, N(t), is the number of discrete elements in a certain set, it is possible to compute the average length of time that an element remains in the set. This is called the mean lifetime.
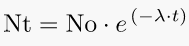
The mean lifetime can be looked at as a “scaling time”, because we can write the exponential decay equation in terms of the mean lifetime.
Nt is the quantity at time t ( number of discrete elements ) (dimensionless), No is the initial quantity (initial population of the assembly) (also dimensionless), e is e, t is time and λ as we said before is the decay constant which is dimensionless as well.

Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.