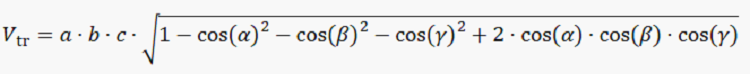Lately Boeing R&D department claimed that they created “the worlds lightest material”, which is also extremely durable.
It is called “microlattice” and it is a synthetic porous metallic material, consisting of an ultra-light metal foam.
What makes it so light you ask my young padawan? Well it is lattice of interconnected hollow tubes with a wall thickness of 100 nanometers, 1,000 times thinner than a human hair. The rest is just air!
It is that strong because its structure is similar to that of a bone, in which the outside is rigid but the inside is mostly hollow, making it lightweight but not easily crushed.
In mathematics, a lattice is a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet).

I searched fxSolver’s database for the “Lattice” keyword and I found this epic formula.

It describes the Triclinic crystal system. In crystallography, the triclinic crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, none of the three vectors are orthogonal to another. The triclinic lattice is the least symmetric of the 14 three-dimensional Bravais lattices. It has (itself) the minimum symmetry all lattices have: points of inversion at each lattice point and at 7 more points for each lattice point: at the midpoints of the edges and the faces, and at the center points. It is the only lattice type that itself has no mirror planes. A crystal is made up of a periodic arrangement of one or more atoms (the basis) repeated at each lattice point. 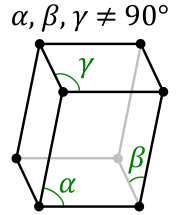Consequently, the crystal looks the same when viewed from any equivalent lattice point, namely those separated by the translation of one unit cell (the motive). The volume of the unit cell can be calculated by the lattice vectors and the angles between the vectors.

Vtr is the volume of the unit cell in triclinic system (in Å3), a the vector (one of the sides of the parallelogram base), b vector (the other side of the parallelogram base), c the vector (one of the edges of the side parallelogram plane) all in Å. α is the angle between b and c vectors, β the angle between a and c vectors and γ the angle between b and a vectors (all in degrees).

Go ahead, check the above formula and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.