Lately, the Ballantine’s Whiskey brand invented a whiskey glass which can be used in zero gravity situations. They call it “Space Glass” and in order to test its functionality they had to use a drop tower.
In physics and materials science, a drop tower or drop tube is a structure used to produce a controlled period of weightlessness for an object under study.
For this experiment, the glass was loaded into the top of the drop tube and it was released to fall to the bottom of the tube. During its flight the sample was recorded with cameras.
The duration of free-fall produced in a drop tube depends on the length of the tube and its degree of internal evacuation. The 105-meter drop tube at Marshall Space Flight Center produces 4.6 seconds of weightlessness when it is fully evacuated.
The Space Glass microgravity experiment took place in the drop facility ZARM in Bremen in a catapult that can be used to throw the experiment upwards to prolong the weightlessness from 4.74 to nearly 9.3 seconds. Negating the physical space needed for the initial acceleration, this technique doubles the effective period of weightlessness. The NASA Glenn Research Center has a 5 second drop tower (The Zero Gravity Facility) and a 2.2 second drop tower (The 2.2 Second Drop Tower).
A formula that is related to this “drop tower” matter is the “Free-fall time” one (Infall of a spherically-symmetric distribution of mass).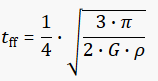
Now go and try using fxSolver, with the free-fall time formula in our database.
Also, remember to follow our social media pages, by hitting the buttons below and watch the fxSolver video as well!
