In our last blog post, we mentioned the scientific mind of a military man, Jean-Charled de Borda, who invented a very smart election method, and his name is on the Borda-Carnot equation.
Today we are digging in the other half of the equation: Nicolas Leonard Sadi Carnot.
Carnot was also a military guy, but the next generations consider him more as an engineer and physicist. His area of expertise was thermodynamics, before thermodynamics were even named that way. He is often described as the “father of thermodynamics”, because he gave the first successful theory of the maximum efficiency of heat engines.
His cycle, “Carnot Cycle” provides an upper limit on the efficiency that any classical thermodynamic engine can achieve during the conversion of thermal energy into work, or conversely, the efficiency of a refrigeration system in creating a temperature difference (e.g. refrigeration) by the application of work to the system. It is not an actual thermodynamic cycle but is a theoretical construct.
The Carnot cycle can be thought of as the most efficient heat engine cycle allowed by physical laws. When the second law of thermodynamics states that not all the supplied heat in a heat engine can be used to do work, the Carnot efficiency sets the limiting value on the fraction of the heat which can be so used.
In order to approach the Carnot efficiency, the processes involved in the heat engine cycle must be reversible and involve no change in entropy. This means that the Carnot cycle is an idealization, since no real engine processes are reversible and all real physical processes involve some increase in entropy.
The equation that describes the Carnot Cycle is the one on the left, where W is the work done by the system (energy exiting the system as work) (J), TH is the absolute temperature of the hot reservoir (K), TC is the absolute temperature of the cold reservoir (K), SB and SA are respectively the Maximum and minimum system entropy (J/K).
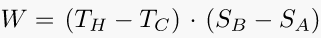
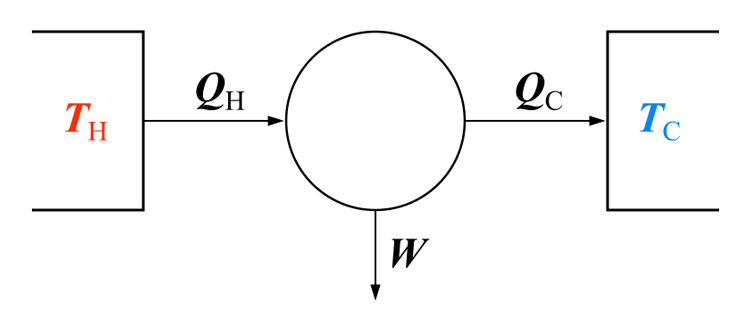
A very interesting aspect of this cycle, is its reversibility. That is, all the processes that comprise it can be reversed, in which case it becomes the Carnot refrigeration cycle. This time, the cycle remains exactly the same except that the directions of any heat and work interactions are reversed. Heat is absorbed from the low-temperature reservoir, heat is rejected to a high-temperature reservoir, and a work input is required to accomplish all this. The P-V diagram of the reversed Carnot cycle is the same as for the Carnot cycle except that the directions of the processes are reversed.
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.