Lasers. We have talked about them two more times in the past. First was the Laser Cutting and the Gaussian beam. Then, the Laser Razor and the Wavelengths of light came by.
In both these stories, the "hot, burning and cutting" laser archetype was confirmed.
We all have in mind that lasers are for cutting things, burn stuff, destroy entire planets, drive your cat crazy and cut James Bond in half.
Some researchers at the University of Washington forgot about all that, thought out of the box and produced the first laser capable of cooling liquids. The technology could be especially useful for slowing down single cells and allow scientists to study biological processes as they happen.
Peter Pauzauskie and team have achieved the first cooling laser in liquids, using an infrared laser to cool water by 36° F (20° C) under normal conditions.
With a brief search in the fxSolver database, I found out the Newton's Law of Cooling. Also known as "Convection-cooling" in cases where the heat transfer coefficient is independent or relatively independent of the temperature difference between object and environment.
Newton’s law, which requires a constant heat transfer coefficient, states that the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings. The rate of heat transfer in such circumstances is derived here.
Newton’s cooling law is a solution of the differential equation given by Fourier’s law
The formula that describes it is the one on the left, where dQ is the thermal energy (Joule), dt the time (sec), h the heat transfer coefficient (W/m2*K), A the surface area of the heat being transferred (m2). Tt is the temperature of the object's surface and interior (since these are the same in this approximation) (K) and Tenv is temperature of the environment; i.e. the temperature suitably far from the surface (K).
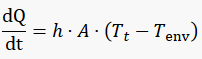
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.