Search results

Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.

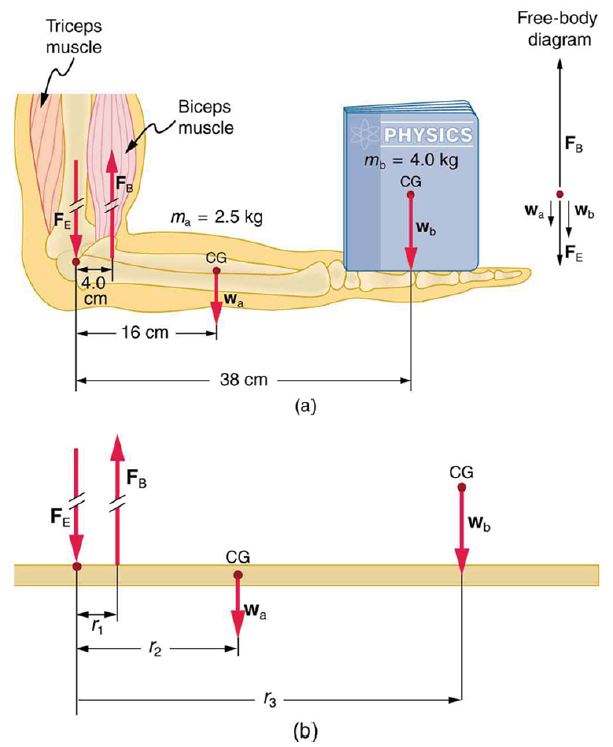
(a) The figure shows the forearm of a person holding a book. The biceps exert a force F_B to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint

Strategy

There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is F_B, that of the elbow joint is F_E, that of the weights of the forearm is w_a , and its load is w_b. Two of these are unknown F_B, so that the first condition for equilibrium cannot by itself yield F_B . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to F_E is zero, and the only unknown becomes F_B .

Solution

The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes

Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for F_B in terms of known quantities,yielding. Entering the known values gives

which yields

Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is

Discussion

This means that the biceps muscle is exerting a force 7.38 times the weight supported.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust T , for the four-rocket propulsion system shown in the Figure below. The sled’s initial acceleration is 49 m/s ², the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.

A sled experiences a rocket thrust that accelerates it to the right.Each rocket creates an identical thrust T . As in other situations where there is only horizontal acceleration, the vertical forces cancel. The ground exerts an upward force N on the system that is equal in magnitude and opposite in direction to its weight,w.The system here is the sled, its rockets, and rider, so none of the forces between these objects are considered. The arrow representing friction ( f ) is drawn larger than scale.
Assumptions: The mass of the Sled remains steady throughout the operation

Strategy

Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.

Solution

Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with

Fnet is the net force along the horizontal direction, m is the rocket’s mass and a the acceleration.

We can see from the Figure at the top, that the engine thrusts add, while friction opposes the thrust.

Tt is the total thrust from the 4 rockets, Fnet the net force along the horizontal direction and Ff the force of friction.

Finally, since there are 4 rockets, we calculate the thrust that each one provides:

T is the individual Thrust of each engine, b is the number of rocket engines

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Calculate the change in length of the upper leg bone (the femur) when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 45.0 cm long and 2.00 cm in radius.

Strategy

The force is equal to the weight supported:

and the cross-sectional area of the upper leg bone(femur) is:

To find the change in length we use the Young’s modulus formula. The Young’s modulus reference value for a bone under compression is known to be 9×10⁹ N/m². Now,all quantities except ΔL are known. Thus:

Discussion

This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 5.3(see reference below) have larger values of Young’s modulus Y . In other words, they are more rigid.

Reference:
This worksheet is a modified version of Example 5.4 page 188 found in :
OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

A typical small rescue helicopter, like the one in the Figure below, has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades.
The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)

Strategy

Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.

Solution for (a)

We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find E_r . The angular velocity ω for 1 r.p.m is

and for 300 r.p.m

The moment of inertia of one blade will be that of a thin rod rotated about its end.

The total I is four times this moment of inertia, because there are four blades. Thus,

and so The rotational kinetic energy is

Solution for (b)

Translational kinetic energy is defined as

To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is

Solution for (c)

At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:

Discussion

The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

(a) Calculate the buoyant force on 10,000 metric tons (1.00×10 7 kg) of solid steel completely submerged in water, and compare this with the steel’s weight.

(b) What is the maximum buoyant force that water could exert on this same steel if it were shaped into a boat that could displace 1.00×10 5 m ³ of water?

Strategy for (a)

To find the buoyant force, we must find the weight of water displaced. We can do this by using the densities of water and steel given in Table [insert table #] We note that, since the steel is completely submerged, its volume and the water’s volume are the same. Once we know the volume of water, we can find its mass and weight

First, we use the definition of density to find the steel’s volume, and then we substitute values for mass and density. This gives :

Because the steel is completely submerged, this is also the volume of water displaced, Vw. We can now find the mass of water displaced from the relationship between its volume and density, both of which are known. This gives:

By Archimedes’ principle, the weight of water displaced is m w g , so the buoyant force is:

The steel’s weight is 9.80×10 7 N , which is much greater than the buoyant force, so the steel will remain submerged.

Strategy for (b)

Here we are given the maximum volume of water the steel boat can displace. The buoyant force is the weight of this volume of water.

The mass of water displaced is found from its relationship to density and volume, both of which are known. That is:

The maximum buoyant force is the weight of this much water, or

Discussion

The maximum buoyant force is ten times the weight of the steel, meaning the ship can carry a load nine times its own weight without sinking.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/