Search results
In geometry, Heron’s formula (sometimes called Hero’s formula), named after Hero of Alexandria, gives the area of a triangle by requiring no ... more
A right triangle (American English) or right-angled triangle (British English) is a triangle in which one angle is a right angle (that is, a 90-degree ... more
In geometry, Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, ... more
A triangle is a polygon with three edges and three vertices. In a scalene triangle, all sides are unequal and equivalently all angles are unequal. The area ... more
An isosceles triangle is a triangle that has two sides of equal length. The area of the isosceles triangle can be calculated by the lengths of the sides.
... more
Triangle is a polygon with three edges and three vertices. The area of a triangle with base length b and height length h is given by multiplying base ... more
Every acute triangle has three inscribed squares (squares in its interior such that all four of a square’s vertices lie on a side of the triangle, so ... more
Stewart’s theorem yields a relation between the length of the sides of the triangle and the length of a cevian of the triangle. A cevian is any line ... more
Related to the length of the sides of the triangle and the radius of the circumcircle of the triangle.
... more
Stewart’s theorem yields a relation between the length of the sides of the triangle and the length of a cevian of the triangle. A cevian is any line ... more
Generalization of the Pythagorean theorem for the side opposite of the acute angle of an arbitrary triangle
... more
Generalization of the Pythagorean theorem for the side opposite of the obtuse angle of an arbitrary triangle
... more
Stewart’s theorem yields a relation between the length of the sides of the triangle and the length of a cevian of the triangle. A cevian is any line ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
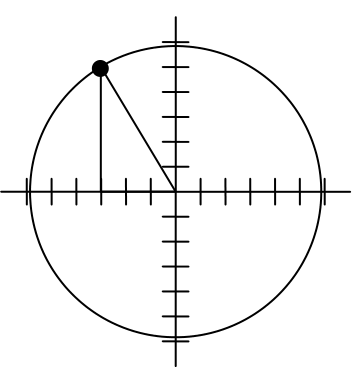
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
The law of cosines relates the cosine of an angle to the opposite side of an arbitrary triangle and the length of the triangle’s sides.
The law
... more
In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, ... more
In mathematics, the Pythagorean theorem, also known as Pythagoras’ theorem, is a fundamental relation in Euclidean geometry among the three sides of ... more
Menelaus’ theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, ... more
The law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.The law of ... more
In hyperbolic geometry, the law of cosines is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar ... more
The interior perpendicular bisector of a side of a triangle is the segment, falling entirely on and inside the triangle, of the line that perpendicularly ... more
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of ... more
Law of sines is an equation relating the lengths of the sides of any shaped triangle to the sines of its angles. The law of sines can be used to compute ... more
Ceva’s theorem is a theorem about triangles in Euclidean plane geometry. Given a triangle ABC, let the lines AO, BO and CO ... more
In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, ... more
Relates the projection of a median and the sides of an arbitrary triangle
... more
An angle bisector of a triangle is a straight line through a vertex which cuts the corresponding angle in half. The three angle bisectors intersect in a ... more
Median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians, one from each ... more
A perimeter is a path that surrounds a two-dimensional shape. The word comes from the Greek peri (around) and meter (measure). The term may be used either ... more
Morley’s trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral ... more
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.