Miller indices calculator (Case of cubic structures)
Description
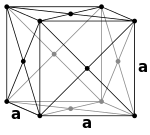
Miller indices form a notation system in crystallography for planes in crystal (Bravais) lattices.
In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written (hkℓ), and each index denotes a plane orthogonal to a direction (h, k, ℓ) in the basis of the reciprocal lattice vectors. For the special case of simple cubic crystals, the lattice vectors are orthogonal and of equal length (usually denoted a); similar to the reciprocal lattice. Thus, in this common case, the Miller indices (hkℓ) simply denote normals/directions in Cartesian coordinates. For cubic crystals with lattice constant a, the spacing d between adjacent (hkℓ) lattice planes can be calculated by the Miller formula.
The lattice constant, or lattice parameter, refers to the physical dimension of unit cells in a crystal lattice. Lattices in three dimensions generally have three lattice constants, referred to as a, b, and c. However, in the special case of cubic crystal structures, all of the constants are equal and we only refer to a. As lattice constants have the dimension of length, their SI unit is the meter. Lattice constants are typically on the order of several angstroms ( For example the lattice constant for a common carbon diamond is a = 3.57 Å at 300 K)
Variables
| dhkl | The spacing d between adjacent (hkℓ) lattice planes (Å) |
| a | The lattice constant (Å) |
| h | Integer (dimensionless) |
| k | Integer (dimensionless) |
| l | Integer (dimensionless) |