Eccentricity of the hyperbola
Description
A hyperbola is a type of smooth curve, lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. ach branch of the hyperbola has two arms which become straighter (lower curvature) further out from the center of the hyperbola. Diagonally opposite arms, one from each branch, tend in the limit to a common line, called the asymptote of those two arms. So there are two asymptotes, whose intersection is at the center of symmetry of the hyperbola, which can be thought of as the mirror point about which each branch reflects to form the other branch.
The shape of a hyperbola is defined entirely by its eccentricity.
Eccentricity denotes the flattening of the hyperbola or how much the hyperbola deviates from an arc of a circle. 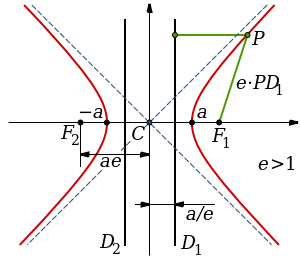
Variables
| ϵ | Eccentricity (dimensionless) |
| c | Distance from the center to a focus (m) |
| a | Distance from the center to a vertex (m) |