Search results
In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square ... more
A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid ... more
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a ... more
In number theory, the sum of the first n cubes is the square of the nth triangular number. The sequence of squared triangular numbers is
0, 1, 9, ... more
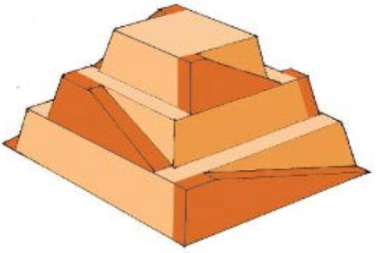
A pyramid frustum is the portion of a pyramid that lies between two parallel planes cutting it.
The volume of a pyramid frustum is related with the
... more
Slant height is the height of any slant triangle of the regular pyramid, or the distance from the apex, down the side, to a point on the base ... more
The Vickers hardness test was developed in 1921 by Robert L. Smith and George E. Sandland at Vickers Ltd as an alternative to the Brinell method to measure ... more
A pyramid frustum is the portion of a pyramid that lies between two parallel planes cutting it. The volume of a pyramid frustum, whose bases are n-sided ... more
A tetrahedron (plural: tetrahedra) is a polyhedron composed of four triangular faces, three of which meet at each vertex. It has six edges and four ... more
a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps, bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 Kcal/hour.
first we calculate the number of hours worked per year.
then we calculate the number of hours worked in the 20 years.
Then we calculate the energy consumed in 20 years knowing the energy consumed per hour and the total hours worked in 20 years.
The efficiency is the resulting potential energy divided by the consumed energy.
...can't find what you're looking for?
Create a new formula
The awe‐inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high (H), with a mass of about 7×10^9 kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging). Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.