Search results
The Brinell scale characterizes the indentation hardness of materials through the scale of penetration of an indenter, loaded on a material test-piece. It ... more
Parabolas with axes of symmetry parallel to the y-axis have equations of the form y=ax^2+bx+c.
The x-coordinate and y-coordinate at the vertex can be
... more
Impulse is the product of a force and the time, for which it acts. The impulse of a force acting for a given time interval is equal to the change in linear ... more
In celestial mechanics, the mean anomaly is an angle used in calculating the position of a body in an elliptical orbit in the classical two-body problem. ... more
Shear rate is the rate at which a progressive shearing deformation is applied to some material. The shear rate for a fluid flowing between two parallel ... more
Ellipse is a curve on a plane surrounding two focal points such that a straight line drawn from one of the focal points to any point on the curve and then ... more
In celestial mechanics, the mean anomaly is an angle used in calculating the position of a body in an elliptical orbit in the classical two-body problem. ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
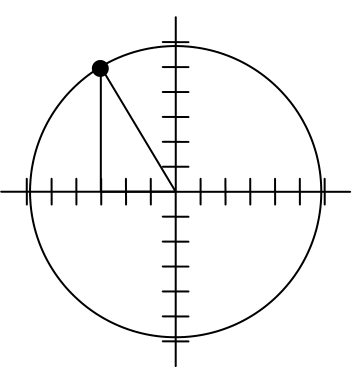
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.