Search results
The weighted mean is similar to an arithmetic mean (the most common type of average), where instead of each of the data points contributing equally to the ... more
In mathematics, the geometric mean is a type of mean or average, which indicates the central tendency or typical value of a set of numbers by using the ... more
Calculates the arithmetic mean size (arithmetic method of moments) of the particles’ size distribution of a soil, in metric scale. In statistics, the ... more
The Heronian mean of two non-negative real numbers is a weighted mean of their arithmetic and geometric means.The weighted mean is similar to an ... more
The arithmetic mean (or simply “mean”) of a sample x1,x2,.x3, ... xn is the sum of the sampled values divided by the number of items in the ... more
Shows how much variation or dispersion from the average exists, on the particles’ size distribution of a soil, in metric scale. Arithmetic mean size (1st ... more
The variance measures how far a set of numbers of n equally likely values is spread out. A small variance indicates that the data tend to be very close to ... more
The standard error (SE) is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that ... more
Arithmetic mean is the sum of a collection of numbers divided by the number of numbers in the collection. The collection is often a set of results of an ... more
Shows how much variation or dispersion from the average exists. Logarithmic mean size (1st moment) needs to be precalculated.
... more
Is a measure that describes the “tailedness” of the probability distribution of a real-valued random variable. Geometric mean size (1st moment) ... more
Is a measure that describes tthe “tailedness” of the probability distribution of a real-valued random variable. Particles logarithmic mean size ... more
In statistics and probability theory, the median is the numerical value separating the higher half of a data sample, a population, or a probability ... more
In mathematics, the harmonic mean (sometimes called the subcontrary mean) is one of several kinds of average. The harmonic mean is the reciprocal of the ... more
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value ... more
Calculates the logarithmic mean size (moments method) of the particles’ size distribution of a soil, in phi scale
... more
In statistics and quantitative research methodology, a data sample is a set of data collected and/or selected from a statistical population by a defined ... more
The gravity of Earth, which is denoted by g, refers to the acceleration that the Earth imparts to objects on or near its surface due to gravity. In SI ... more
Heat capacity or thermal capacity is a physical quantity equal to the ratio of the heat that is added to (or removed from) an object to the resulting ... more
Log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. The standard ... more
In mathematics, generalised means are a family of functions for aggregating sets of numbers, that include as special cases the arithmetic, geometric, and ... more
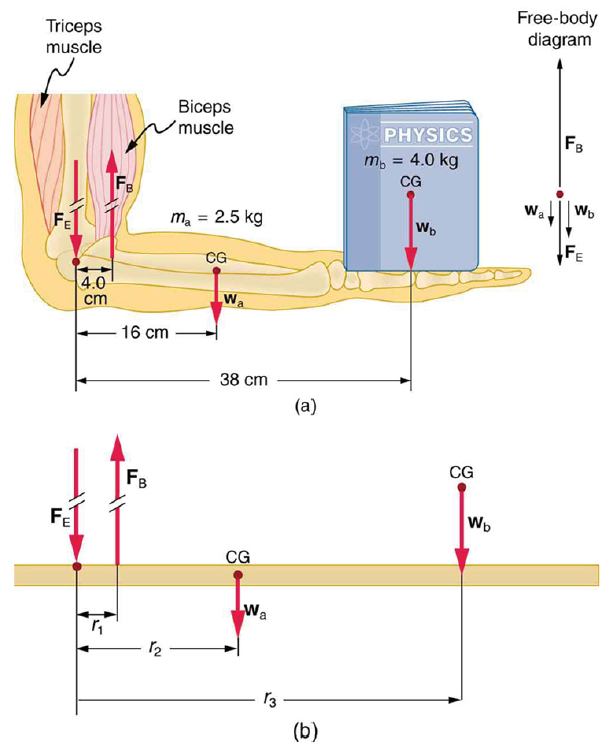
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
The awe‐inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high (H), with a mass of about 7×10^9 kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging). Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.
a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps, bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 Kcal/hour.
first we calculate the number of hours worked per year.
then we calculate the number of hours worked in the 20 years.
Then we calculate the energy consumed in 20 years knowing the energy consumed per hour and the total hours worked in 20 years.
The efficiency is the resulting potential energy divided by the consumed energy.
a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. A random ... more
In statistics and probability theory, the median is the numerical value separating the higher half of a data sample, a population, or a probability ... more
Heat capacity or thermal capacity is a physical quantity equal to the ratio of the heat that is added to (or removed from) an object to the resulting ... more
Heat capacity or thermal capacity is a physical quantity equal to the ratio of the heat that is added to (or removed from) an object to the resulting ... more
Specific impulse (usually abbreviated Isp) is a measure of the efficiency of rocket and jet engines. By definition, it is the impulse delivered per unit of ... more
Birch’s law establishes a linear relation of the compressional wave velocity of rocks and minerals of a constant average atomic weight with density ... more
...can't find what you're looking for?
Create a new formula
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.