It is impressive how things were working back in the day! If someone was really smart and was wealthy enough, he would become whatever he wanted. All at once!
When I searched for Borda-Carnot equation, which is a really interesting one, I found out that it was named after Jean-Charles, chevalier de Borda and azare Nicolas Marguerite, Comte Carnot.

The first, Jean-Charled de Borda, was a military man (a Sailor), but he was also a brilliant mathematician, physicist and political scientist.
He fought in the American Revolutionary War, he was captured by the enemy and after his release he started fixing and improving waterwheels and pumps. After that he introduced a massive construction program to revitalize the French navy.
He also came up with the “Borda count”. An election method in which voters rank the candidates in order of preference. In the end only one is the winner, but the point system of this method usually elects the broadly acceptable candidate rather than the one preferred by the majority. The Borda count is used usually for decision making and not for electing representatives of any kind.

In fluid dynamics the Borda–Carnot equation is an empirical description of the mechanical energy losses of the fluid due to a (sudden) flow expansion. The Borda–Carnot loss equation is only valid for decreasing velocity, v1 > v2, otherwise the loss ΔE is zero – without mechanical work by additional external forces there cannot be a gain in mechanical energy of the fluid.

The loss coefficient ξ can be influenced by streamlining. For example in case of a pipe expansion, the use of a gradual expanding diffuser can reduce the mechanical energy losses.
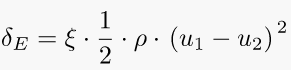
The equation is the one on the left where δE is mechanical energy loss of the fluid per unit of fluid volume (J/m3), ξ is empirical loss coefficient , 0 ≤ ξ ≤ 1(dimensionless), ρ is the fluid density (kg/m3), and υ1 and υ2 are the mean flow velocities before and after expansion respectively (m/s).
There are some variations of this equation which we are going to discuss in our next post.

Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.