The latest Star Wars movie is so epic that we are almost obligated to make at least 7 Star Wars posts to honor its existence!
We Started with the Star Wars and Black Holes Episode I, which is containing some minor spoilers for the latest movie, just like the Episode II. On Episode I we analyzed the Black Hole Surface Gravity equation, and on Episode II we talked about Schwarzschild radius. In Episode III we discussed the energy distribution of emission which is described by Planck’s law and we also compared the attributes of a Black Hole in the Star Wars Universe with our world’s Black Holes. In Episode IV, Stephen Hawking was the man of the hour and his Radiation energy.
Today, we are talking Density.
The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein’s field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density and pressure. The equations for negative spatial curvature were given by Friedmann in 1924.

In the Star Wars Universe, a device similar to a tractor beam generator, just like the one Death Star operators used to capture the Millennium Falcon in episode III, is called "Density projector". The projector can increase an item's density. Using this device on a Battle Droid allows it to effectively anchor itself where it stood. An ultra battle droid with its density projector active was virtually impossible to knock down, even for a Jedi using the Force.
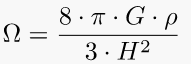
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.
