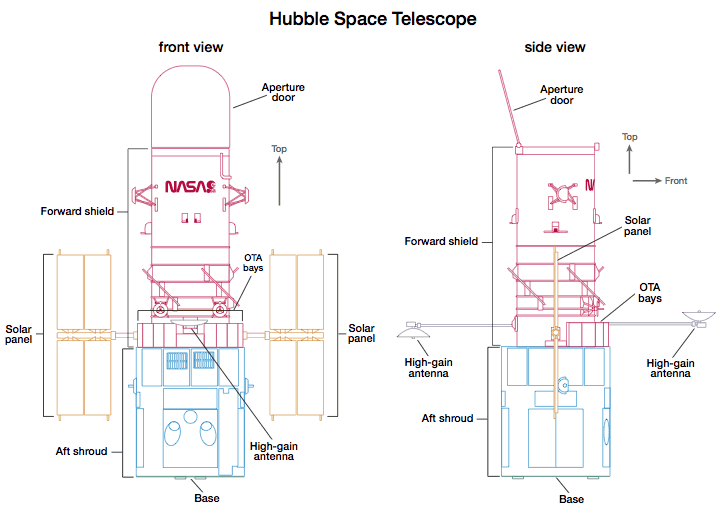
Remember the fancy Hubble Space telescope? It was launched into low Earth orbit in 1990, and its 2,4 meter mirror observes the near ultraviolet, visible and near infrared spectra.
Its orbit just outside the distortion of earth’s atmosphere, allows it to take extremely high-resolution images with negligible background light.
It has recorded some of the most detailed visible-light images ever, allowing a deep view into space and time. Many Hubble observation lead to breakthroughs in astrophysics.
Now, NASA is manufacturing its successor, the James Webb Space Telescope (JWST).
It is scheduled to launch in 2018, and it will be capable of viewing the very first generation of stars that ignited in the early Universe. It’ll be used to investigate the formation of early galaxies, study the evolution of our own solar system, look at distant worlds, and much more. If it’s anything like its predecessor, it’ll have a huge impact on humanity’s knowledge of the Universe.
I browsed fxSolver’s database and found a formula that calculates the calculates the Magnification of the Telescope.
Optical magnification is the ratio between the apparent size of an object (or its size in an image) and its true size, and thus it is a dimensionless number.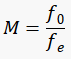
A telescope uses its large objective lens to create an image of a distant object and then allows the user to examine the image closely with a smaller eyepiece lens thus making the object look larger.
An eyepiece, or ocular lens, is the lens that is closest to the eye when someone looks through the device. The objective lens or mirror collects light and brings it to focus creating an image. The eyepiece is placed near the focal point of the objective to magnify this image.
The angular magnification of the telescope is related to the focal length of the objective lens and the focal length of the eyepiece. M is the magnification (dimensionless), f0 the focal length of the objective lens and the fe the focal length of the eyepiece (cm).
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.