There is a video trending these days which is titled “How to go to Space, in Simple Words”. They creators are trying to explain the whole concept of how a person can go to space using only the 1000 most used words in the English Language.
It may sounds simplistic and probably great to watch, but it ends up being funny and sometimes confusing! Enjoy the video!

So, now you know what you need to get into an Up-Go-er, which is pushed to space by fire-water, you should probably need to read some more fancy words about space.

How about “Vis-viva”. Sounds sophisticated right?

Vis Viva is Latin for “Live force” (May the Vis be with you, my young Padawan!) It is also a term from the history of mechanics, and it survives in this sole context. It represents the principle that the difference between the aggregate work of the accelerating forces of a system and that of the retarding forces is equal to one half the vis viva accumulated or lost in the system while the work is being done.
In astrodynamics, the vis-viva equation, also referred to as orbital-energy-invariance law, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy which applies when the only force acting on an object is its own weight.

There is the Vis-Viva Equation regarding the orbital speed. Where ν is the relative speed of the two bodies (m/s), r is the distance between the two bodies, G the Newtonian constant of gravitation, M the mass of the central body(Kg), and a the semi-major axis (in meters, just like “r”).

There is an alternate version of the above formula called Vis-Viva Equation – with standard gravitational parameter, and it uses the standard gravitational parameter instead of the Newtonian constant of gravitation and the mass of the central body. It is obviously the one on the left, and μ is the standard gravitational parameter (m³/s²).

The Vis-Viva Equation is a bit different when it comes to circular orbit. It is simple as the formula you see on the left, where μ is the standard gravitational parameter and r is the distance between the two bodies (in meters).

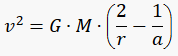
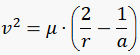
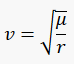
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.