In 2006, important astronomers gathered in Prague, to solve a major issue of their science. What is a planet, and what it’s not?
They ended up with these 3 criteria.
1. It has to be in orbit around the Sun,
2. it has sufficient mass to assume hydrostatic equilibrium (well, to have a nearly round shape), and
3. it has “cleared the neighborhood” around its orbit.
The first two are pretty much clear. What about the third? 
What a planet should do to clear the neighborhood around its orbit? Make a Neighborhood watch? Well no. It means that it has to be a big bully, and get rid any other orbiting objects apart from its satellites around it. In more scientific words, it has to become gravitationally dominant, and there are no other bodies of comparable size other than its own satellites or those otherwise under its gravitational influence.
If a large body in space, meets the first two criteria but has not cleared its neighborhood is classified as a dwarf planet.
This criterion threw Pluto out of our Planetary system, and made it a dwarf planet.
How a (potential) planet can clear its neighborhood. Over many orbital cycles, a large body will tend to cause small bodies either to accrete with it, or to be disturbed to another orbit, or to be captured either as a satellite or into a resonant orbit. As a consequence it does not then share its orbital region with other bodies of significant size, except for its own satellites, or other bodies governed by its own gravitational influence. This latter restriction excludes objects whose orbits may cross but that will never collide with each other due to orbital resonance, such as Jupiter and its trojans, Earth and 3753 Cruithne, or Neptune and the plutinos.
In their paper, Stern and Levison sought an algorithm to determine which “planetary bodies control the region surrounding them”. They defined Λ (lambda), a measure of a body’s ability to scatter smaller masses out of its orbital region over a long period of time. Λ is a dimensionless number defined by the equation on the left. M is the mass of the body, a is the body’s semi-major axis, and k is a function of the orbital elements of the small body being scattered and the degree to which it must be scattered. In the domain of the solar planetary disc, there is little variation in the average values of k for small bodies at a particular distance from the Sun.
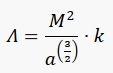
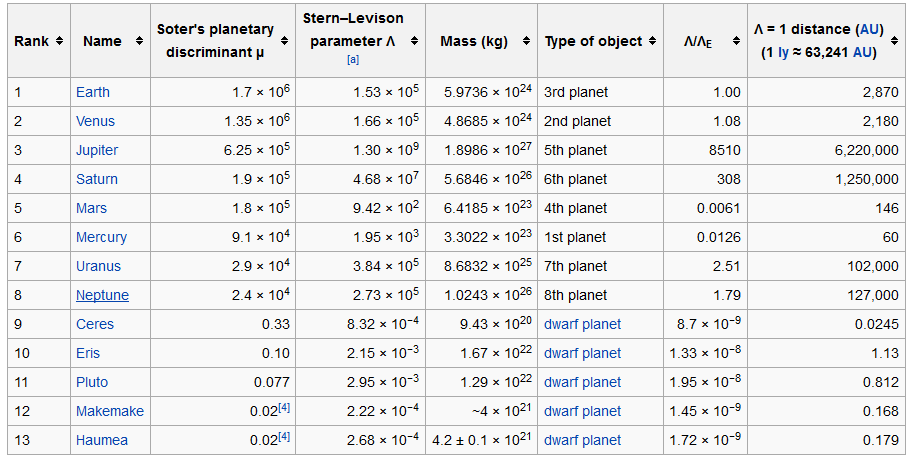
If Λ > 1, then the body will likely clear out the small bodies in its orbital zone (you can check the table below for our solar system’s Λs). Stern and Levison used this discriminant to separate the gravitionally rounded, Sun-orbiting bodies into überplanets, which are “dynamically important enough to have cleared its neighboring planetesimals”, and unterplanets. The überplanets are the eight most massive solar orbiters (i.e. the IAU planets), and the unterplanets are the rest (i.e. the IAU dwarf planets).
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.
