Discovered in 1930, Pluto was long considered our solar system’s ninth planet. But after the discovery of similar intriguing worlds deeper in the distant Kuiper Belt, icy Pluto was reclassified as a dwarf planet. This new class of worlds may offer some of the best evidence about the origins of our solar system. Although some astronomers believe Pluto should still be considered a planet.
Pluto has five known moons: Charon (the largest, with a diameter just over half that of Pluto), Styx, Nix, Kerberos, and Hydra. Pluto and Charon are sometimes considered a binary system because the barycenter of their orbits does not lie within either body.
In 2006, NASA’s New Frontiers program, launched an interplanetary space probe named New Horizons in order to study Pluto, its moons and the Kuiper Belt, performing flybys of the Pluto system and one or more Kuiper Belt Objects. It was launched into an Earth-and-solar-escape (Escape Velocity) trajectory with an Earth-relative speed of about 16.26 kilometers per second (58,536 km/h; 36,373 mph); it set the record for the highest launch speed of a human-made object from Earth.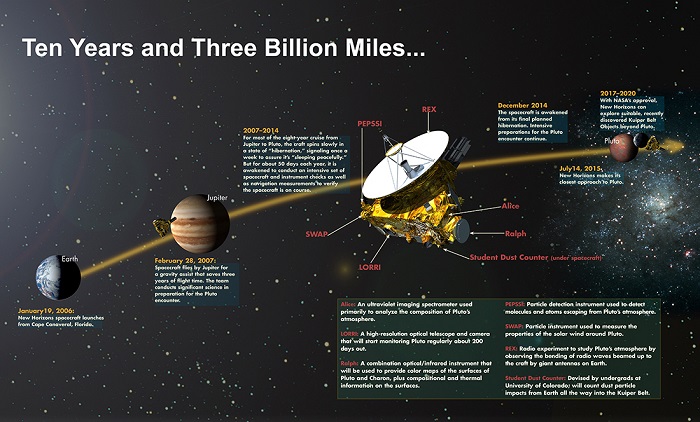

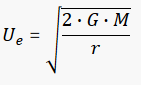
Escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero. It is the speed needed to “break free” from a gravitational field without further propulsion. For a spherically symmetric massive body, the escape velocity at a given distance can be calculated by the mass of the massive body(M), and the distance from the center of gravity®. Atmospheric friction (air drag) is not taken into account.
“Escape velocity” is the initial speed required to go from an initial point in a gravitational potential field to infinity with a residual velocity of zero, with all speeds and velocities measured with respect to the field.

Finally after a decade-long journey through our solar system, New Horizons made its closest approach to Pluto Tuesday, about 7,750 miles above the surface making it the first-ever space mission to explore a world so far from Earth. You probably have seen all these amazing pictures on the internets. If not, check this link.

As always, you can try using fxSolver, with the Escape velocity formula in our database.
Please, remember to follow our social media pages, by hitting the buttons below and watch the fxSolver video as well!