In fluid mechanics, the Reynolds number (Re) is a dimensionless quantity that is used to help predict similar flow patterns in different fluid flow situations. The concept was introduced by George Gabriel Stokes in 1851, but the Reynolds number is named after Osborne Reynolds (and not Ryan Reynolds), who popularized its use in 1883. Well, it’s not the first thing that takes the name of the advertiser and not the inventor.
The Reynolds number is defined as the ratio of momentum forces to viscous forces and consequently quantifies the relative importance of these two types of forces for given flow conditions.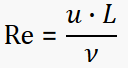
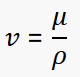
u: mean velocity of the object relative to the fluid (m/s), L: characteristic linear dimension (m), ν: Kinematic viscosity (m2/s)
First we have to calculate ν, the kinematic viscosity. Viscosity is a property arising from collisions between neighboring particles in a fluid that are moving at different velocities. When the fluid is forced through a tube, the particles which comprise the fluid generally move more quickly near the tube’s axis and more slowly near its walls: therefore some stress, (such as a pressure difference between the two ends of the tube), is needed to overcome the friction between particle layers and keep the fluid moving. For the same velocity pattern, the stress required is proportional to the fluid’s viscosity. Viscosity is a measure of the resistance of a fluid which is being deformed by either shear stress or extensional stress. The kinematic viscosity is defined as the dynamic viscosity of a fluid divided by its density. μ: Dynamic Viscosity (N*s/m2), ρ: Density (kg/m3).
Then we Substitute values into the equation for N’R and there it is.
Click on to the links to see and understand more about what we described doing. It is so much easier that way. Then you can try create your own worksheet. There are instructions all over the place, and a video that explains everything.
Remember to follow our social media pages, by hitting the buttons below!