Surprisingly, the most exciting part of a Moto GP for an amateur watcher, is neither the high speed nor the “spectacular” crashes. It’s the incredible lean angles the riders reach at every corner, in order to get through it as fast as possible.
Over the years, the tire companies improved their technology so much, that a biker can lean up to 64º from upright. Consider that an everyday bike user leans about 40º to 50º and think how awesome is what the professionals are doing.
You seem unimpressed! You ask “why not lean over more”?
Well, at first let us say that you are ungrateful, and then explain.
The edges of the tires are made of rubber which is less directly supported by the inflated fabric within (carcass). This makes them more flexible and in order to get enough grip to support both cornering and acceleration, the rider tries to hold the bike more upright, using a part of the tread that is directly supported by the carcass.
Has leaning any formulas? Of course it has!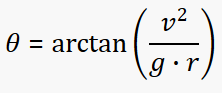 
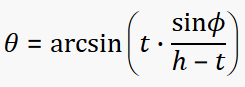
First, is just “Leaning”. Leaning during a turn happens to balance the relevant forces, which are: gravitational, inertial, frictional, and ground support. The angle of lean can be calculated using the laws of circular motion. θ is the angle of lean (radians), ν The forward speed (m/s), g the Standard gravity, and r the radius of the turn (in meters).
Then, it’s the “Lean angle due to a tire thickness”. The finite width of the tires alters the actual lean angle of the rear frame from the ideal lean angle described above. The actual lean angle between the frame and the vertical must increase with tire width and decrease with center of mass height. Bikes with fat tires and low center of mass must lean more than bikes with skinnier tires or higher centers of mass to negotiate the same turn at the same speed.The increase in lean angle due to a tire thickness of 2t can be calculated by the ideal lean angle and the height of the center of mass. Θ is the Lean angle (degrees), t is the Half tire thickness (inch), φ the ideal lean angle (degrees) and h the Height of the center of mass (inch).
Don’t forget, that you can add the equations to the fxSolver, with just a few clicks!
Also, remember to follow our social media pages, by hitting the buttons below!